(Some notes on black holes information problem)

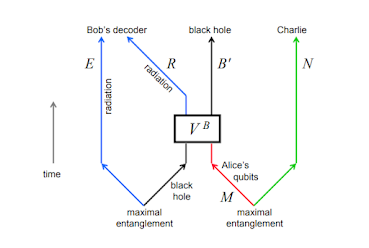
At the moment, black holes and their information diary are intriguing theoretical physics problems. Starting with Hawking-Bekenstein, it is a very engaging problem, which has taken multiple routes over the course. To name a few- unitarity, holography (or AdS-CFT correspondence), and page theorem. Page theorem (and page curve) was one of the most exciting developments. 

Page curve suggests that the radiation $R$ is still maximally entangled with the remaining black hole $BH$. At the page time, both coarse-grained entropy is equal as $S_R = S_{BH}$, and after page time, as for a pure state, the entropy of the black proceeds to zero. It is very profound if you think hard about it. Page curve is a part of the hotter debate of whether infalling information is conserved in the radiation. 

Recovering the information (of course, this is just theoretical because an actual black hole information experiment is out of technical reach) is an arduous task and should be done quantum mechanically. I encountered Hayden and Preskill's experiment in https://arxiv.org/abs/1409.1231 (which I suggest for taking a broad view of the problem). Hayden and Preskill throw a diary in the black hole, and the diary is entangled to a system, early radiation, and black hole is entangled. After the black hole consumes the diary, in a thermalized sense, the question is how fast the information comes out. The answer, among others, is (http://arxiv.org/abs/0708.4025v2) very rapidly for black holes that have already radiated by half (in other words, black holes which have exceeded the page time). This led them to call old black holes as mirrors.

Arrangement of Hayden and Preskill's. From http://arxiv.org/abs/0708.4025v2