We have five categories of consistent string theory;
- Type I
- Type IIA
- Type IIB
- Heterotic $E_8 \times E_8$
- Heterotic $SO(32)$
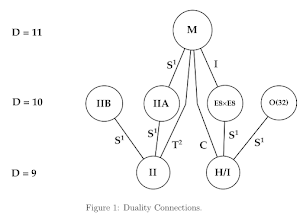
Type I has both closed and open strings. Type IIA and Type IIB contain only oriented closed strings. Heterotic strings are hybrid of bosonic string theory and superstring theory. There are two of them and much interesting. There are many striking relations between all of them, which were worked out by Sagnotti, Sen, Witten, Polchinski, and a few others. We call these relations dualities. (A critical, relating gauge/gravity theory, duality came from Maldacena in 1997, where he proved that Type IIB in AdS is equivalent to N=4 SYM on the conformal boundary.)
Type IIB is dual to Type I by T-duality. Type IIA and Type IIB are related by T-duality. T-duality relates theories on different tori. (T-duality is a very interesting duality that comes up when we have a compactification, as in toroidal compactification.) Type I with g coupling and Heterotic SO(32) with 1/g coupling are related by S-duality. Mirror symmetry relates string theories compactified on other Calabi-Yau manifolds. Compactification of Type II on a K3 Calabi-Yau manifold is dual to Heterotic theories on the 4-torus. Taking the limit $g\rightarrow \infty$ of Type IIA gives 11d Supergravity. These were significant results given that string theory was thriving for something like these dualities, which proved that all are merely the same string theory in different limits or on different geometry.