The Way Theorized

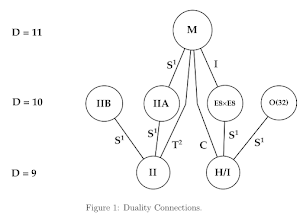
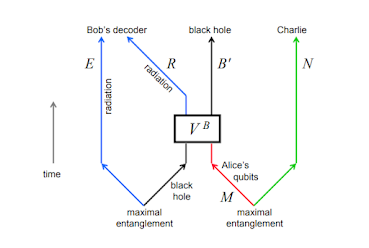
Let us take a look at Yoneda Lemma, which might be the most trivial yet the hardest part of Category theory (and algebraic geometry). I would not be drawing any commutative diagrams.

Let us say we have an analytic function $f(z)$ where $z \in \mathbb{C}$ defined in a tube $T$

This is a three pages note on two papers - Scheme for reducing decoherence in quantum computer memory by Peter W. Shor and Error detecting and error correcting codes by R.W Hamming. The latter is about a parity check, and the former is about a quantum error check.

I wrote some discussions on the black information problem. Unfortunately, I could not include the AdS/CFT solution to the information problem while I strongly insist on studying it, do consider Harlow Jerusalem's review paper for that.

Since the 1970s, black holes have emerged as a central area for theorists. Here are five points why.

Joseph (Joe) Gerard Polchinski Jr. was an exceptional physicist who gave a lot to string theory. He has inspired a generation of physicists. He is personally one of my string heroes. In his later life, he suffered from cancer that made him unable to even read. Despite all the constraints, he wrote his autobiography and posted it on arXiv in 2017; you may read it here. Ahmed Almheiri (Joe's student) recently edited the biography to add more scientific explanations and image plates. There is a forward by Andrew Strominger and afterward by Joe's family. The book has been published by MIT Press. 

Recently, I spotted a rough yet beautiful representation of the formation, evaporation, and different stages of black holes in https://arxiv.org/abs/2006.06872, which is an excellent review to read. I am reproducing it here.

We have five categories of consistent string theory;

Type IIB is dual to Type I by T-duality. Type IIA and Type IIB are related by T-duality. T-duality relates theories on different tori. (T-duality is a very interesting duality that comes up when we have a compactification, as in toroidal compactification.) Type I with g coupling and Heterotic SO(32) with 1/g coupling are related by S-duality. Mirror symmetry relates string theories compactified on other Calabi-Yau manifolds. Compactification of Type II on a K3 Calabi-Yau manifold is dual to Heterotic theories on the 4-torus. Taking the limit $g\rightarrow \infty$ of Type IIA gives 11d Supergravity. These were significant results given that string theory was thriving for something like these dualities, which proved that all are merely the same string theory in different limits or on different geometry.

Another relevant figure from https://arxiv.org/pdf/hep-th/9607201.pdf

After reading Harlow's review notes on the black hole information problem, I am convinced that there could be many ways to explain the black holes information problem and black holes interior. It would be worth waiting and seeing which one is correct and which is less accurate. Here, I want to collect those possible ways of describing BHs.

I wrote some notes on information theory and its application in quantum mechanics and computing. I acknowledge D. Dhar for his constant support throughout the period.

Notes on Information Theory

Recently, I strolled around an exciting fact about a difference of meaning of covariant and contravariant words in mathematics (category theory) and physics (tensor analysis). Well, that makes it harder for a mathematician and a physicist to talk about these two words without knowing in what sense.

In category theory, we can think of functors as the mapping of objects between categories. We can say that if a functor preserves the direction of morphism, then the functor is a covariant one. If it reverses the direction of the morphism, then it is a contravariant functor. John Baez has briefly mentioned them in his book "Gauge Fields, Knots and Gravity". An identity functor is a covariant functor, and so are tangent vectors. While cotangent vectors and 1-forms are contravariant. (1-form in this case is differential of a function, however, if a differential of a function is to be thought as a vector field then the vector fields are covariant.)

Suppose we have a map $\phi:M \rightarrow N$ from one manifold to another. On $N$, we have real valued functions defined from $\psi:N\rightarrow \mathbb{R}^n$. To get real valued functions on $M$ we have pullback $\psi$ from $N$ to $M$ by $\phi$. 

$$\phi * \psi = \psi \circ \phi$$

We see that real-valued functions on $M$ suffer a change of direction in their morphism. So they are contravariant.

In tensor analysis, one can say that $X_\mu$ is covariant and $X^\mu$ is contravariant. (It is important to dodge that $\partial_\mu$ is covariant while its component $v^\mu$ can be contravariant.)

Here is my 10 pages handwritten (rough) notes on Heterotic string theory. We will work on both $SO(32)$ and $E_8 \times E_8$. For any reference, one can use String Theory Vol 1 and Vol 2 by Green, Schwarz and Witten. 

Heterotic Strings

Entropy $S(x)$ is the measure of randomness of a variable $x$. It is important in the area of information theory, which, on the other hand, shares similarities with the entropy that we have in thermodynamics. We write entropy as

$$S(x) =\sum -p(x) \log p(x),$$

here $p(x)$ is the probability mass distribution of the variable. In quantum information theory (or quantum Shannon theory), we use discrete matrices in the place of mass distribution. We mostly prefer the logarithms in base 2 and the entropy is measured in bits. 

Suppose that Alice has sent a message which contains either $a$ or $b$. There is half-chance probability occurring of either. In this case, the binary entropy looks like the below figure, where when $p=1/2$ and $(1-p)=1/2$ the entropy becomes $1$ bit,

$$S(x)=-p(x)\log p(x) - (1-p) \log (1-p),$$

For more than one variable, we have joint entropy

$$S(x,y) = -\sum_{x}\sum_{y} p(x,y) \log p(x,y)$$

If, for instance, Alice sends a message consisted of strings a and b

$$ababcbcbcba$$

then the messaged received by Bob is given by conditional entropy which is given by conditional probability

$P_{x \mid y}\left(x_{i} \mid y_{j}\right)=\frac{P_{x, y}\left(x_{i}, y_{j}\right)}{P_{y}\left(y_{j}\right)}$

and (we change the notation a bit, calling $X,Y$ random variable)

$$I(X; Y)=\sum_X \sum_Y p(x,y) \log \frac{p(x,y)}{p(x)p(y)} = S_{X}-S_{X Y}+S_{Y}$$

is the mutual information between two variables $X,Y$. The mutual information ($I(X;Y)$) is given by the relative entropy of the joint probability mass function and the product distribution given by $p(x)p(y)$ (I will recommend T. Cover and J. Thomas, Elements Of Information Theory. John Wiley Sons, 2006, for introductory materials.)

A look at general $x\log x$.

Winter is here and so the holidays and breaks. Here, I include few papers that might be interested to you to read in this winter break. In no specific order. Theme- Random Matrices and JT gravity.

•   JT gravity as a matrix integral by Phil Saad, Stephen Shenker and Douglas Stanford - https://arxiv.org/abs/1903.11115.
  

•  Nonperturbative Jackiw-Teitelboim gravity by Clifford V. Johnson and his other papers on this subject as well- https://arxiv.org/abs/1912.03637. 
  

•  Lower dimensional gravity by Roman Jackiw- https://doi.org/10.1016/0550-3213(85)90448-1.

•  Gravitation and hamiltonian structure in two spacetime dimensions by Claudio Teitelboim- https://doi.org/10.1016/0370-2693(83)90012-6.
  

• Comments on the Sachdev-Ye-Kitaev model by Juan Maldacena, Douglas Stanford- https://arxiv.org/abs/1604.07818.
  

• JT Gravity and the Ensembles of Random Matrix Theory by Douglas Stanford, Edward Witten- https://arxiv.org/abs/1907.03363.

Some bonus recommendations ;)

• Newly appeared paper by Ed Witten on Quantum field theory in curved spacetime (https://arxiv.org/abs/2112.11614). There are also lectured by him on the same on Youtube.
  

• Anna Karenina by Leo Tolstoy.
  

I simulated Albert Einstein with GPT-3. The best that I could. Here is the conversation we had. I have edited some stuff, I did not include anything, but all quite was fun.

Here are a few hot topics in high-energy physics. Not in any order. Moreover, of course, they are biased from my eye-view of hep-th.

Some basics of complex analysis. We will follow L. Ahlfors's Complex Analysis book. An analytic function is a complex-valued function with derivatives everywhere where function $f(x)$ is defined with an appropriate power series. Holomorphic functions are the same, with a different meaning. For an analytic function $f(z) = u+iv$, we write

It is a common misconception that renormalization is needed only when infinities are coming up. But R. Shankar beautifully tackles this in his textbook on Quantum Field Theory and Condensed Matter in chapter 11th. 

We will take a $4 \times 4$ random unitary matrix of Gaussian nature (Hermitian ensemble) -  generated from Mathematica.

One may now do many things with this matrix, such as generating its Gaussian distribution. 

There are many common misconceptions (or carelessness) that amateur string readers have. One of those is that bosonic string theory on worldsheet is for bosons, and superstring theory on superspace is for fermions (well, only fermions). This is technically wrong. Superstring theory has both bosonic sector (with Neveu-Schwarz - NS- boundary condition) and fermionic sector (with Ramond boundary condition). However, the NS bosonic sector (which uses the same $X^\mu$ worldsheet of the free bosonic theory of D=26) of Superstring is different from the bosonic theory in D=26. One of the things that differentiate the two is the presence of an extra oscillator in the former.  NS bosonic sector does not have the critical dimension $26$ but $10$.

In superstring theory, we add an extra wave-function $\psi^\mu$ which is related to $X^\mu$ by world-sheet supersymmetry (space-time SUSY is used in GS formalism). The fermionic sector (of course of Superstring) is also ghosts-free at $D=10$. And the Virasoro algebra of the free bosonic theory is replaced by the Super-Virasoro algebra.

I have been lately studying the random matrices and their application that widely defaults for the JT gravity. Though, random matrices need to be started with Wigner's idea of the random matrix in nuclear theory. Right now, random matrix theory can be considered an important subject, at least from my learning view. In the following (short), I present my rough ideas of random matrix theory, extracted from here.

Random matrix theory (RMT) is a classic example of statistical group theory in general physics. The most recent development for RMT is the equivalence of JT gravity with RMT, see here. From the correspondence of AdS/CFT, one learns that a bulk theory with gravity lives on the boundary of a quantum system. However, the equivalence of JT gravity is not given to a boundary theory (or a bulk theory). In fact, RMT shares the correspondence with JT gravity; hence JT gravity is dual to random matrix integral of Hamiltonian $ H $, where $ H $ is a random matrix.

(RMT is mainly concerned about groups' statistics, at least for us, whose applications are wide in physics, as indicated.)

Consider a matrix $ \sf M $, from linear algebra we know that $ \sf M$ holds eigenvalues $ {\sf {m}}_{ij} $ (for $ 2 \times 2 $ matrix). Suppose the elements of matrix $ \sf M $ are random variables, to which we say to obey some specific outlined properties. In that case, the study of those ($\mathsf{m}_{ij} $) eigenvalues are called the "random matrix theory'' problem. Now one can ask what the practical application of RMT is. Actually, there are many practical applications. Consider the well-studied example of the nucleus using these random matrices, which Wigner (and Dyson) developed. And the recent example of the success of RMT is JT gravity. I suggest the reader to read the most interesting book on this subject by  Madan Lal Mehta.

Let us catch with some updates. 

• Susskind has a good paper on de-Sitter space here. He has been pretty active in de-Sitter lately. One should first start with his and colleagues' paper on the causal patch and then follow up on his recent writings. (I recently saw a video of Susskind highly appraising Juan Maldacena here.)
• I wrote a fine and short piece of introduction (and basically mixed up) article on field theory and beyond, which can be found here and here.
• Subir Sachdev, TIFR, and IAS have organized a course on Quantum phases of matter. The lectures can be viewed at http://qpt.physics.harvard.edu/qpm/.
• Breakthrough Prizes have been awarded https://breakthroughprize.org/News/65.